Playing with Gravity to Learn CUDA: A 2-Body Simulation

In the last post of this series on learning CUDA through building a gravity simulation, we didn't actually do any CUDA. We focused on defining gravity and figuring out how we were going to actually simulate it with practical equations. Now it's time to put those equations to work and see if we can come up with a functioning simulation that uses CUDA. We'll start with the simple 2-body problem of the Earth orbiting around the Sun, and see if we can keep the Earth in orbit.

The Kernel

Remember, the part of the code that executes on the GPU is the kernel. We're going to start with designing the kernel because I want to get the gravity equations down in code in order to get a handle on which vectors we're going to need to supply to the kernel from the host CPU. We'll build up the rest of the simulation from that kernel, and then we can see how it works. 

First, we need to think about how this kernel is going to be used during execution. Each thread running on the GPU will execute its own instance of the kernel. We will have n bodies in this simulation, and each body will need to examine every other body to calculate their contribution to the total gravitational force felt by the first body. Said another way, if we have bodies b₁, ..., b_n, then we calculate the total force on body b₁ from the contributions of the forces from bodies b₂, ..., b_n. It may seem from this O(n²) problem that we could gain something by parallelizing every individual body-body calculation, but if n is on the order of the number of cores in the GPU, then we've really gained nothing but difficulty in designing the calculations in the kernel because we're going to have to do n iterations anyway. The iterations are just no longer in a simple inner loop in the thread of one body calculation. We may even suffer a slowdown from too much extra control code to manage everything. It'll be simpler and likely sufficient to have the kernel do the whole calculation for one body, and the simulation will be O(n) as long as n is on the order of the number of cores in the GPU.

With that consideration out of the way, we'll start with the gravitational constant, and a simple data structure to hold a 2D point:

#include "cuda_runtime.h"
#include "device_launch_parameters.h"

#include <stdio.h>

#define G 6.674e-11

typedef struct vec2d {
    float x;
    float y;
} vec2d;

The includes are the basic CUDA includes that all such programs require, and G is our gravitational constant from the last post. The vec2d struct simply contains x and y elements, and it's intended to be used in vector calculations. It's guaranteed to pack neatly into arrays since there's no extra fluff, and we're going to need that compactness when passing data to and from the GPU.

Next, for the kernel definition we're going to need the mass and current position of each body, the current velocity of the body we're calculating, and we'll output the new position and velocity of that body. All of these variables are passed to the kernel as arrays of data for all bodies because all of the data is loaded into the GPU memory at once, and each thread instance will access the elements that it needs to. The start of the kernel then looks like this:

__global__ void gravityKernel(vec2d* v, vec2d* d, const float *m, const vec2d* v0, const vec2d* d0, float dt)
{
    int i = threadIdx.x;
    const vec2d d0_i = d0[i];
    vec2d a = { 0, 0 };

The first thing we need to do in the kernel is grab the index for the thread that's currently running. That index threadIdx will allow us to access the correct location in the arrays for the body we're calculating the force on for this thread. We then immediately pull out the current location for that body for easy access during the rest of the calculation. We also initialize a vector for the acceleration for that body, and this vector will accumulate all of the contributing accelerations from the forces from each other body in the simulation. The for loop that follows contains this accumulated acceleration calculation derived from the gravitational force and acceleration formulas from the last post:

    for (int j = 0; j < blockDim.x; j++) {
        if (j == i) continue;

        const vec2d d0_j = d0[j];
        vec2d r_ij;
        r_ij.x = d0_i.x - d0_j.x;
        r_ij.y = d0_i.y - d0_j.y;

        float r_squared = r_ij.x * r_ij.x + r_ij.y * r_ij.y;

        float F_coef = -G * m[i] * m[j] / r_squared;
        vec2d F_ij;
        F_ij.x = F_coef * r_ij.x * rsqrtf(r_squared);
        F_ij.y = F_coef * r_ij.y * rsqrtf(r_squared);

        a.x += F_ij.x / m[i];
        a.y += F_ij.y / m[i];
    }

This code may look like complicated math, but it's a straight translation of the two force equations in vector form:

F = ma

First, we calculate the r_ij vector for the distance from body j to body i (the direction is important), and then just churn through the rest of the equations. The rsqrtf() function calculates 1 / sqrtf(), which is faster to do as the reciprocal and then multiply instead of doing the divide by the square root directly. Note that we multiply by m[i] to calculate F_coef, and then we divide by the same m[i] later to calculate the acceleration vector to add, so we can remove those operations and accumulate the acceleration vectors more directly:

    for (int j = 0; j < blockDim.x; j++) {
        if (j == i) continue;

        const vec2d d0_j = d0[j];
        vec2d r_ij;
        r_ij.x = d0_i.x - d0_j.x;
        r_ij.y = d0_i.y - d0_j.y;

        float r_squared = r_ij.x * r_ij.x + r_ij.y * r_ij.y;

        float F_coef = -G * m[j] / r_squared;
        a.x += F_coef * r_ij.x * rsqrtf(r_squared);
        a.y += F_coef * r_ij.y * rsqrtf(r_squared);
    }

Another thing to note in this code is that blockDim.x is another standard variable from CUDA that gives the size of the block of threads, which in this case translates directly to the number of bodies. It's a convenient variable to use as the loop boundary. Then right at the beginning of each loop instance, we check if the opposing body we're looking at is the same as the one we're calculating the acceleration for, and we skip to the next body in that case. Otherwise, we'll get a divide-by-zero error when we divide by r_squared. The rest of the kernel simply calculates the new velocity and position vectors:

    const vec2d v0_i = v0[i];
    v[i].x = v0_i.x + a.x * dt;
    v[i].y = v0_i.y + a.y * dt;

    d[i].x = d0_i.x + v0_i.x * dt + a.x * dt * dt / 2;
    d[i].y = d0_i.y + v0_i.y * dt + a.y * dt * dt / 2;
}

There should be no surprises there.

Calling the Kernel

On the next level up in the code, we need to call the kernel from the host CPU. We'll use a helper function to call the kernel and read the newly computed position vector out of the GPU memory:

cudaError_t gravityIter(vec2d* d, vec2d* dev_v, vec2d* dev_d, const float* dev_m, const vec2d* dev_v0, const vec2d* dev_d0, float dt, unsigned int size)
{
    cudaError_t cudaStatus;

    // Launch a kernel on the GPU with one thread for each body.
    gravityKernel <<< 1, size >>> (dev_v, dev_d, dev_m, dev_v0, dev_d0, dt);

    // Check for any errors launching the kernel
    cudaStatus = cudaGetLastError();
    if (cudaStatus != cudaSuccess) {
        fprintf(stderr, "addKernel launch failed: %s\n", cudaGetErrorString(cudaStatus));
        return cudaStatus;
    }

    // cudaDeviceSynchronize waits for the kernel to finish
    cudaStatus = cudaDeviceSynchronize();

    // Copy output vector from GPU buffer to host memory.
    cudaStatus = cudaMemcpy(d, dev_d, size * sizeof(vec2d), cudaMemcpyDeviceToHost);
    
    return cudaStatus;
}

This code differentiates between GPU device memory variables and host CPU memory variables with the "dev_" prefix for GPU variables. That way, we can keep straight where any given variable resides, as that's critically important. Trying to access variables in the wrong memory space will cause a crash. We go ahead and call gravityKernel right away in this function, passing the GPU device variables that it needs and size for the number of threads to create in the special kernel call syntax. Then we check for errors, call a cudaDeviceSynchronize() command to wait for the kernels to finish, and call cudaMemcpy() to copy the position vector on the GPU back to the host CPU memory. The first three arguments should look familiar to anyone that's used memcpy() before, and the final cudaMemcpyDeviceToHost argument specifies which direction we're copying this data.

I showed one example of the error checking code for cudaGetLastError() to give a sense of what basic error checking looks like, but I left out the rest for conciseness. Basically anywhere that cudaStatus is set would have similar error handling. It's useful for debugging if something goes wrong, but uninteresting otherwise. On the next level up, we want to call this gravityIter() function from a loop that will step the gravity simulation. Here's what that looks like:

cudaError_t gravitySim(vec2d* d, const float* m, const vec2d* v0, const vec2d* d0, const float dt, unsigned int size, unsigned int iterations)
{
    float* dev_m = 0;
    vec2d* dev_v0 = 0;
    vec2d* dev_d0 = 0;
    vec2d* dev_d = 0;
    vec2d* dev_v = 0;
    cudaError_t cudaStatus;

    // Choose which GPU to run on, change this on a multi-GPU system.
    cudaStatus = cudaSetDevice(0);
    if (cudaStatus != cudaSuccess) {
        fprintf(stderr, "cudaSetDevice failed!  Do you have a CUDA-capable GPU installed?");
        goto Error;
    }

    // Allocate GPU buffers for five vectors (three input, two output)    .
    cudaStatus = cudaMalloc((void**)&dev_d, size * sizeof(vec2d));
    cudaStatus = cudaMalloc((void**)&dev_v, size * sizeof(vec2d));
    cudaStatus = cudaMalloc((void**)&dev_m, size * sizeof(float));
    cudaStatus = cudaMalloc((void**)&dev_v0, size * sizeof(vec2d));
    cudaStatus = cudaMalloc((void**)&dev_d0, size * sizeof(vec2d));

    // Copy input vectors from host memory to GPU buffers.
    cudaStatus = cudaMemcpy(dev_m, m, size * sizeof(float), cudaMemcpyHostToDevice);
    cudaStatus = cudaMemcpy(dev_v0, v0, size * sizeof(vec2d), cudaMemcpyHostToDevice);
    cudaStatus = cudaMemcpy(dev_d0, d0, size * sizeof(vec2d), cudaMemcpyHostToDevice);

    int time = 0;
    printf("Time,Object0.x,Object0.y,Object1.x,Object1.y\n");
    for (int i = 0; i < iterations; i++) {
        if (cudaSuccess != (cudaStatus = gravityIter(d, dev_v, dev_d, dev_m, dev_v0, dev_d0, dt, size))) {
            goto Error;
        }

        time += dt;
        printf("%d,%f,%f,%f,%f\n", time, d[0].x, d[0].y, d[1].x, d[1].y);

        if (cudaSuccess != (cudaStatus = gravityIter(d, dev_v0, dev_d0, dev_m, dev_v, dev_d, dt, size))) {
            goto Error;
        }

        time += dt;
        printf("%d,%f,%f,%f,%f\n", time, d[0].x, d[0].y, d[1].x, d[1].y);
    }

Error:
    cudaFree(dev_d);
    cudaFree(dev_v);
    cudaFree(dev_m);
    cudaFree(dev_v0);
    cudaFree(dev_d0);

    return cudaStatus;
}

Okay, there's quite a bit here to go through, but it's pretty straightforward. We're doing all of the GPU device setup here as well as iterating the simulation, so the device setup happens first. We declare the device variables, set which device we're using, allocate all of the memory on the device, and copy the data to the device for the input vectors. Again, I showed the first example of error handling and omitted the rest. Yes, this code is using gotos to jump to the end of the function on an error and free up any memory that has been allocated. That's how the template did it, and I just stuck with it. It could be easily changed by making one more level of function call that returned the error code and the memory could be freed at that level to keep everything clean and goto-free. I figured this use of gotos was pretty innocuous for a short piece of code.

Now we're at the crux of the function—the iterations. The number of iterations is actually doubled in this for loop, and the reason to call gravityIter() twice in this way is that it makes it easy to ping-pong between the current and next velocity and position vectors. Notice that dev_v and dev_d are swapped with dev_v0 and dev_d0 between the two calls. This swap makes the previous call's new velocity and position vectors the next call's initial velocity and position vectors, and the other vectors can be used for the new new data that will be calculated. At the top of the next iteration, the variables get swapped again automatically. No temporary variables necessary!

The last thing I want to mention is the printf() statements. They're used to get the positions out to the debug console for, well, debugging purposes, and I can graph the data in a spreadsheet for an easy visual display. However, this method of getting data out of the program will not be sustainable because printing to the console in the middle of a simulation is very slow. We'll cook up something better in the future.

Initializing the Simulation

All that's left to do is initialize some variables in main() and call that last gravitySim() function. I saved the easiest for last:

int main()
{
    const int arraySize = 2;
    const float m[arraySize] = { 1, 2 };
    const vec2d d0[arraySize] = { {0, 0}, {1, 0} };
    const vec2d v0[arraySize] = { {0, 0}, {0, 1} };
    vec2d d[arraySize] = { {0, 0}, {0, 0} };
    const float dt = 1;
    const unsigned int iterations = 10;

    // Run gravity simulation.
    cudaError_t cudaStatus = gravitySim(d, m, v0, d0, dt, arraySize, iterations);
    if (cudaStatus != cudaSuccess) {
        fprintf(stderr, "gravitySim failed!");
        return 1;
    }

    // cudaDeviceReset must be called before exiting in order for profiling and
    // tracing tools such as Nsight and Visual Profiler to show complete traces.
    cudaStatus = cudaDeviceReset();
    if (cudaStatus != cudaSuccess) {
        fprintf(stderr, "cudaDeviceReset failed!");
        return 1;
    }

    return 0;
}

These variable initializations are meant to create a simple simulation that I can easily see is correct. The masses of the bodies are so small that they should have no effect on the acceleration or velocity of either body, and I should see the first body stay at (0, 0) while the second body flies upward (in the y-direction) at 1 m/s. Since dt is 1 second, it should reach y = 20 m. And we can see it works perfectly:

Cool beans, it worked! I bet you were surprised. Time to try something more ambitious.

Earth Orbiting the Sun

Let's try plugging in the values for the mass of the Sun and the Earth, the average distance of the Earth from the Sun in the x direction, and the average velocity of the Earth in the y direction (values found at Wikipedia):

    const float m[arraySize] = { 1.989e30, 5.972e24 };
    const vec2d d0[arraySize] = { {0, 0}, {1.496e11, 0} };
    const vec2d v0[arraySize] = { {0, 0}, {0, 2.978e4} };
    vec2d d[arraySize] = { {0, 0}, {0, 0} };
    const float dt = 86400;
    const unsigned int iterations = 183;

Mass is in kg, distance in meters, velocity in m/s, and time in seconds. Those values are a heckuva lot bigger than before, and they should produce a gravitational effect that will be seen in the calculations. These values give a step time of one day, and a simulation time of just over one year, because the iterations are doubled. So what do we get?

Well, um. That doesn't look quite right. I mean, the Earth is definitely going around the Sun, and the Sun is staying put in the center (at least at this scale). Yet, the Earth doesn't complete a full orbit in a year, and it kind of looks like it's going to spiral out from there. What's the problem? Well, it turns out that simulations that use differential equations are extremely dependent on the resolution of the time step, among other things. This happens to be a simulation of differential equations. You can tell by the dt variable. That delta-time is a dead giveaway that we're dealing with a difficult simulation problem.

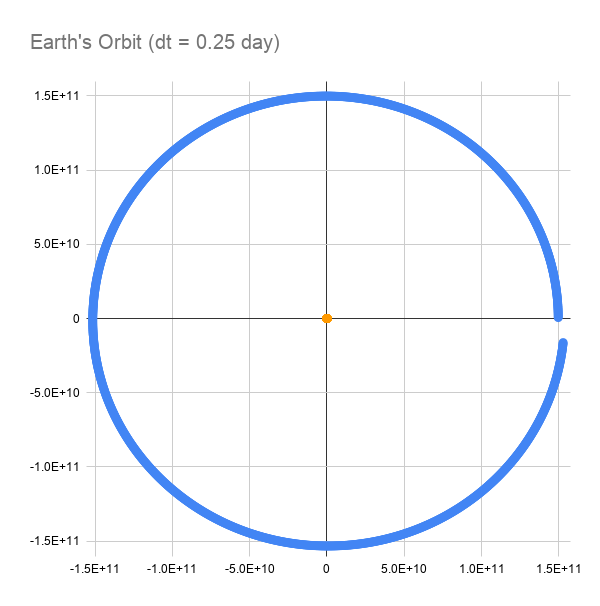
We can increase the accuracy of the simulation by decreasing the time step. That means, instead of assuming that the Earth is going to maintain its calculated acceleration and velocity for a full day, we're going to narrow that timeframe to six hours—a quarter of a day. In reality, the Sun's gravity has a continuous effect on the Earth, and vice versa, so the acceleration and velocity are changing continuously, but I don't have all day to run this simulation. I just want to see if we can get an improvement. Here's the exact same simulation with a time step of 21,600 seconds and 732 (really 1464) iterations:

This is looking promising. We still don't complete a full orbit, but we're much closer. I'm sure dropping the time step to half an hour or ten minutes or something will get us close enough for practical purposes. What about that Sun-dot in the middle; what does that look like?

What the heck is that?! It looks like the Sun swings out 800,000 meters (800 km) and comes back 300 km "up" from where it started. I know the Earth exerts some pull on the Sun, along with all of the other planets, that causes it to wobble around, but I would expect it to look more like a circle. The issue here is likely initial conditions. The Sun shouldn't start motionless, and in fact, it should start with an initial velocity in the negative y direction, opposite the Earth's velocity. That should give this motion a more circular path. Another possible way to see that circular path is to extend the simulation for much longer. The Sun and the Earth should settle into a stable orbit with the Sun having a small circular wobble. This simulation shows another important point about these types of simulations, namely that the initial conditions matter–a lot. I know I've seen these things mentioned in books and on websites, but it really brings it home to see it in a simulation you've built yourself. Another thing that I expect has an effect, although smaller than the time step or initial conditions for this particular simulation, is the finite resolution of the 32-bit floats. The resolution of the data, and the rounding error of the calculations could be improved by using doubles, but the trade-off is a slower simulation. That resolution problem is going to have an effect at extremely long time scales, which is why it's so hard to simulate the solar system accurately out to more than a few thousand years. For our purposes, I'll stick with floats until it becomes obvious that we need the extra resolution.

This was all very exciting to get a simulation up and running on my graphics card using CUDA. I would like to explore this simulation of Earth's orbit some more, but it's tedious to keep exporting the data from the console to a spreadsheet and plotting it. Next time we'll look at plotting the simulation in realtime (or at least simtime) with a visual display. I mean, I'm already programming the graphics card, might as well use it for graphics, too. The visual display will also enable us to explore more complicated simulations in the future. Right now the simulation isn't quite right for more than two bodies, but that will come after we can see it on the screen.