Adding the Second Algorithm
The first thing we need to do to add a second algorithm into the mix is add an ability to change the algorithm type, both within the UI and in the code when running the solver. The UI addition is easy. All we need to do is replace the "Round Robin" text with a <select> tag that includes the <option> tags for each algorithm choice we'll support. Right now that will be "Round Robin" and "Random Choice," since a random algorithm will be another simple algorithm that will be quick to implement. I also gave the <select> tag an ID of solver_type, so it can easily be accessed from the code.
The code changes are a little more extensive than the UI. We'll start with adding an event handler to update the solver state when the algorithm changes. For that addition we can add this code to the Solver.init() function:
$('#solver_type').change(function () {
switch (this.value) {
case 'roundrobin':
that.solverType = that.roundRobin;
break;
case 'random':
that.solverType = that.randomChoice;
break;
default:
that.solverType = that.roundRobin;
break;
}
game_moves = [];
seed = 1;
makeBlocks();
});We should also set an initial value for the solverType so that it's ready to go when the page loads, and we can stick that near the bottom of Solver, after the definition of the algorithms:
function Solver() {
// ...
this.roundRobin = function() {
// ...
}
this.solverType = this.roundRobin; this.solver = $('<div>', {
id: 'solver',
class: 'control btn',
style: 'background-color:' + colors[this.index]
}).on('click', function (e) {
that.solverType();
}).appendTo('#solver_container'); this.run = function _run() {
that.solverType();
// ...
} this.randomChoice = function() {
controls[this.index].updateGameBoard();
this.index = randomInt(0, controls.length - 1);
this.solver.css('background-color', colors[this.index]);
} this.runAlgorithm = function() {
controls[this.index].updateGameBoard();
this.solverType();
this.solver.css('background-color', colors[this.index]);
}
this.roundRobin = function() {
this.index = (this.index + 1) % controls.length;
}
this.randomChoice = function() {
this.index = randomInt(0, controls.length - 1);
}Notice how this architecture came about naturally. I didn't spend a lot of time trying to plan out the perfect set of functions ahead of time. I added things incrementally, and as optimization and organizational changes became obvious, I did them. Too much planning and design runs the risk of architecting the code into a dead end, making it difficult to add new features to a code base that has become too complicated with twists and turns that form a maze of objects and function calls. I much prefer taking a path of least resistance, paying attention to where the code is leading, and making incremental improvements that organize and support the code for the problem it is attempting to solve.
Some programmers may balk at the use of a switch statement to decide which algorithm to use, but it's not as bad as it seems. Switch statements get cumbersome when there are multiple switch statements operating on similar objects with similar structure strewn throughout the code. These switch statements all have to be updated whenever another item is added to the list of possible cases. If you ever find yourself updating multiple switch statements when adding a new option or feature, that's the time to think about how to reorganize that code into a class hierarchy so that most of the switch statements can be eliminated. Most of the time, you'll still need one switch to create the objects from the correct classes, but one should be enough. I don't expect to need more than this one switch statement for the different types of algorithms, so I think it's fine.
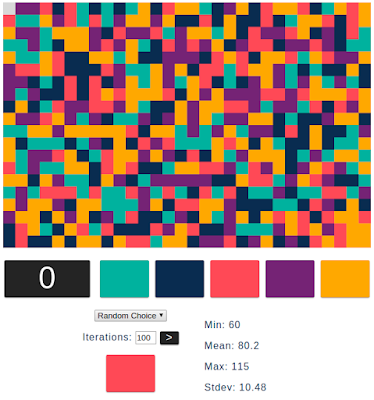
Getting back to this new random choice algorithm, let's see how it performs:
Wow, that is much worse than round-robin was. The average number of moves is 30 moves higher than round-robin, and the standard deviation is twice as big. Here's a comparison of the two algorithms:
| Round Robin | Random Choice | |
|---|---|---|
| Min | 37 | 60 |
| Mean | 48.3 | 80.2 |
| Max | 62 | 115 |
| Stdev | 4.5 | 10.5 |
It's also apparent when watching the algorithm run that it behaves differently. It sometimes appears to get stuck, pausing for a moment before continuing to clear blocks. It also seems to leave some colors of blocks behind for a while while it clears others. Both of these behaviors are caused by the randomness of the algorithm. It appears to pause when it repeatedly picks the same color more than once, and certain colors will appear to get left behind if the algorithm happens to not pick them for an extended sequence of moves. Not picking one color for a long time may not be much of an issue, but picking the same color multiple times in a row is definitely contributing to this algorithm's poor performance. We should start looking at how to improve that behavior.
Improving Random Choice with Skipping
The immediate problem of picking the same color more than once in a row is fairly easy to solve. We can add a new algorithm type to the drop-down selector with the option value of "random-skip," and then add a case to the switch statement for it:
$('#solver_type').change(function () {
switch (this.value) {
case 'round-robin':
that.solverType = that.roundRobin;
break;
case 'random':
that.solverType = that.randomChoice;
break;
case 'random-skip':
that.solverType = that.randomChoiceWithSkipping;
break;
default:
that.solverType = that.roundRobin;
break;
} this.randomChoiceWithSkipping = function() {
i = randomInt(0, controls.length - 1);
while (this.index === i) {
i = randomInt(0, controls.length - 1);
}
this.index = i;
}Everything has improved, with the average number of moves being reduced by 17 moves, and the standard deviation being reduced by nearly 3 moves. However, this is still substantially worse than the round-robin algorithm, and that's likely because of how the random choice algorithm picks colors differently than round-robin. Because it's possible that the next random color that's chosen was the same as one picked in the recent past, it's more likely that the chosen color doesn't remove any more blocks, or at least very few. The round-robin algorithm guarantees that at least the next color will be the least recently picked color, and it's likely that more blocks of that color will be exposed for removal by the time the color comes around again.
We aren't going to consider optimizing the number of blocks removed on each color choice quite yet. That's getting into a different kind of algorithm, but we can look at not picking a color that will not remove any blocks on the current move. That would still be a random algorithm with skipping, and it seems like it would further improve the random choice algorithm. We're kind of going for the most non-wasteful random algorithm we can think of here, while still keeping it as random as possible.
So how do we check that the candidate random color removes at least one block? The current code doesn't lend itself well to this check because the tasks of finding blocks to remove, removing those blocks, and incrementing the move count all happen together in the same base function call. There's no way to easily check for a color without also doing the rest of the work of updating the game board. Luckily, there's a fairly simple way to get what we want by adding a function and threading a conditional parameter through the function calls for updating the blocks. I can imagine that at some point we're going to want to separate out those search and update tasks because later algorithms are going to do a deeper, more complex search of the board, but by then we'll also want to change the data structure for the blocks. That's a bigger change to the code that isn't really necessary, yet, so let's stick with the simple workaround for now.
To implement the simple workaround, we want to create a function that does most of what Control.updateGameBoard() does, except for the updating the game board part. Instead of searching for blocks of a certain color adjacent to grey blocks and removing them, we want to search for blocks of a certain color adjacent to grey blocks and return whether a match was found. To do this check, we can start by updating the algorithm to do what we want it to do, and then fill in the details as we go:
this.randomChoiceWithSkipping = function() {
do {
this.index = randomInt(0, controls.length - 1);
} while (controls[this.index].checkGameBoard(true) === false);
} function Control(color) {
// ...
this.updateGameBoard = function() {
this.checkGameBoard(false);
if (isFinished()) {
game_moves.push(moves + 1);
makeBlocks();
} else {
moves += 1;
}
$('.score').text(moves);
}
this.checkGameBoard = function(only_check) {
var match = false;
var color = this.color;
_.each(blocks, function (block) {
if (block.isDead) {
match = match || getNeighbors(block, color, only_check);
}
});
return match;
}You've probably noticed that this code is a little wasteful in that it does not return on the first match found. It will continue searching through the rest of the grey blocks even after finding a match. While that's probably less efficient, there is a reason for it. I'm still working from the assumption that we're going to want to completely change the method of searching for colors later on because the current method will prove to be too slow. I don't want to do that change until I need to, though, so I'm doing the simplest thing that will work here without changing too much code. It's still fast enough for these simple algorithms, and I have a hunch that if we change things to return immediately on a match, we'll be changing it back in the near future for the greedy algorithm. Let's move on to the changes to getNeighbors():
function getNeighbors(block, color, only_check) {
// ...
return checkNeighbors(neighbor_positions, color, only_check);
}
function checkNeighbors(positions, color, only_check) {
var match = false;
_.each(positions, function (position) {
var block = blocks[position];
if (block.color == color && !block.isDead) {
if (only_check) {
match = true;
return;
}
block.isDead = true;
$('#block' + position).css('background-color', '#d9d9d9');
getNeighbors(block, color, only_check);
}
});
return match;
}The enhanced skipping should now be working, so let's give it a whirl:
Things have improved yet again! Now we're getting pretty close to the performance of round-robin, as we can see in the following table:
| Round Robin | Random Choice | Random with Skipping | |
|---|---|---|---|
| Min | 37 | 60 | 43 |
| Mean | 48.3 | 80.2 | 53.1 |
| Max | 62 | 115 | 64 |
| Stdev | 4.5 | 10.5 | 4.5 |
The fact that random choice with skipping is still slightly worse than round-robin probably means that the least-recently-used behavior of round-robin is slightly more optimal than just picking a color at random. This is good. We now have two reasonable baselines for comparing against future algorithms. We do have one more improvement we can make, however.
Improving Round-Robin
Clearly, now that we can skip colors that aren't worth choosing in random choice because they won't remove any blocks, we can do the same thing with round-robin. This is an easy addition, and it should improve round-robin's performance somewhat. To add this algorithm, we can create another menu choice, add it to the switch statement, and add this algorithm code:
this.roundRobinWithSkipping = function() {
do {
this.index = (this.index + 1) % controls.length;
} while (controls[this.index].checkGameBoard(true) === false);
}Not as much as I was expecting, but it's still an improvement. Let's look at all of the results:
| Round Robin | RR with Skipping | Random Choice | Random with Skipping | |
|---|---|---|---|---|
| Min | 37 | 37 | 60 | 43 |
| Mean | 48.3 | 46.9 | 80.2 | 53.1 |
| Max | 62 | 59 | 115 | 64 |
| Stdev | 4.5 | 4.1 | 10.5 | 4.5 |
We shaved 1.4 moves off of the average, 3 moves off of the max, and 0.4 moves off of the standard deviation, showing that the distribution tightened up somewhat. I'll bet most of the improvement by not picking dead colors in round-robin came from the beginning and the end of games, when there are most likely to be less useful colors to pick from.
Now we should have a good idea of what to expect from future algorithms. A normal game with haphazard choices of colors will result in about 50 moves, if we at least take care to not pick a color that won't remove any blocks. Picking a color that was not picked recently is also generally better than picking a color totally at random. The goal for the rest of the algorithms is to do better than this, much better. We should also start to get an idea of what a reasonable lower bound is for the number of moves in a typical game, and thus, what a well-played game looks like. We'll start down that path next time with the greedy algorithm, and see where that takes us.
Article Index
Part 1: Introduction & Setup
Part 2: Tooling & Round-Robin
Part 3: Random & Skipping
Part 4: The Greedy Algorithm
Part 5: Greedy Look Ahead
Part 6: Heuristics & Hybrids
Part 7: Breadth-First Search
Part 8: Depth-First Search
Part 9: Dijkstra's Algorithm
Part 10: Dijkstra's Hybrids
Part 11: Priority Queues
Part 12: Summary



No comments:
Post a Comment